18 SparseIndexedPowerProduct
This file contains an implementation polynomials in the variables x1,x2,… over
the rational numbers. Such polynomials are well suited as cycle index polynomials
(cf. [BLL98, Appendix 1]).
The tests can be found in test/poly/idxpp.as.nw.
505⟨* 13⟩+
≡ ⊲462 525 ⊳
-------------------------------------------------------------------
----
---- Combinat
---- Copyright (C) Ralf Hemmecke <ralf@hemmecke.de>
---- svn co svn://svn.risc.uni-linz.ac.at/hemmecke/combinat/
----
-------------------------------------------------------------------
#include "combinat"
⟨dom: SparseIndexedPowerProduct 506⟩
Type Constructor
SparseIndexedPowerProduct
Description
Implements power products in arbitrarily many variables.
Let V be an (ordered) set of variables. Variables can be thought of being
x1,x2,…, but SparseIndexedPowerProduct does not provide a way to define the
symbol that is used for the variables and E be the (additive) monoid of
possible exponents. Then SparseIndexedPowerProduct implements the monoid
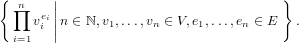 |
(180)
|
The exports of SparseIndexedPowerProduct are the multiplicative counterparts of
the ones from IndexedFreeAdditiveCombinationType.
Remarks
Different variables pairwise commute, i. e., if v1,v2 ∈ V with v1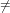 v2 then
v1e1v2e2 = v2e2v1e1. However, depending on whether the + operation in E is
commutative or not it could well be that
v2 then
v1e1v2e2 = v2e2v1e1. However, depending on whether the + operation in E is
commutative or not it could well be that
Of course, it is also allowed, that
ve1ve2 = 1, if
e1 +
e2 = 0 in
E.
506⟨dom: SparseIndexedPowerProduct 506⟩≡ (505)
SparseIndexedPowerProduct(
V: TotallyOrderedType, -- VariableType
E: TotallyOrderedType with {
zero?: % -> Boolean;
+: (%, %) -> %;
}
): with {
⟨exports: SparseIndexedPowerProduct 509a⟩
} == add {
macro {
X == rep x;
Y == rep y;
}
Rep == SparseAdditiveArray(E, V);
import from Rep, E, V;
⟨implementation: SparseIndexedPowerProduct 509b⟩
}
Defines:
SparseIndexedPowerProduct, used in chunks 55, 103a, 307, 526, 562, 564, 566, 567, 626,
665, 707, 710–17, 719, 721, 723, 725–27, 744–47, 749, 751c, and 753.
Uses SparseAdditiveArray 489 and TotallyOrderedType 571.
Exports of SparseIndexedPowerProduct
-
-
TotallyOrderedType;
-
-
1: % Returns the multiplicative identity.
-
-
one?: % -> Boolean Returns true if the power products contains no variable.
-
-
*: (%, %) -> % Multiplies two power products.
-
-
power: (V, E) -> % Returns a power of a certain variable.
-
-
generator: % -> Generator Cross(E, V) Generates exponent-variable pairs starting with
the biggest variable.
-
-
map: (Cross(E, V) -> Cross(E, V)) -> % -> % Applies a function to all (exponent,
variable) pairs.
-
-
if E has with {-: (%, %) -> %; -: % -> %} then {
-
-
/: (%, %) -> % Divides two power products.
-
-
}
-
-
if E has with {0: %} then {
-
-
apply: (%, V) -> E Extracts the exponent corresponding to some variable.
-
-
}
-
-
if E has with {0: %; next: % -> %} then {
-
-
divisors: % -> Generator % Generates all divisors.
-
-
}
-
-
if V has with {weight: % -> E} and E has with {0: %; *: (%, %) -> %} then {
-
-
weight: % -> E Computed the weight of a power product.
-
-
}
-
-
if V has OutputType and E has OutputType then OutputType;
Note that we have chosen MachineInteger as the type for the variable index
as well as for the exponents. The reason is that we will store a a sum of
cycle index polynomials at entry w of a formal power series where w is given
by the weight of the cycle index polynomial. Since FormalPowerSeries
can realistically store not more then max@MachineInteger=2147483647
values (∼ 2 ⋅ 109), the above choice for SparseIndexedPowerProduct is
sufficient.
509b⟨implementation: SparseIndexedPowerProduct 509b⟩≡ (506) 509c ⊳
(x: %) = (y: %): Boolean == X = Y;
509c⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲509b 510 ⊳
(x: %) < (y: %): Boolean == X < Y;
512b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲511b 513b ⊳
one?(x: %): Boolean == zero? X;
513b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲512b 514b ⊳
(x: %) * (y: %): % == per(X + Y);
Export of SparseIndexedPowerProduct
power: (V, E) -> %
Description
Returns a power of a certain variable.
The function call power(v,e) returns ve.
Remarks
The function returns 1 if the given exponent e is zero.
514b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲513b 515b ⊳
power(v: V, e: E): % == if zero? e then 1 else per [e, v];
Export of SparseIndexedPowerProduct
generator: % -> Generator Cross(E, V)
Description
Generates exponent-variable pairs starting with the biggest variable.
Remarks
The call generator(1) returns a generator that generates no element.
Export of SparseIndexedPowerProduct
map: (Cross(E, V) -> Cross(E, V)) -> % -> %
Description
Applies a function to all (exponent, variable) pairs.
Remarks
This function assumes that the given function that is applied to coefficient and
index does not destroy the order, i. e., we assume that in map(f,x) the function
f : E × V → E × V is monotone in its second argurment; if (e1′,v1′) = f(e1,v1)
and (e2′,v2′) = f(e2,v2) and v1 < v2 then v1′ < v2′.
516a⟨exports: SparseIndexedPowerProduct 509a⟩+
≡ (506) ⊲515a 516c ⊳
map: (Cross(E, V) -> Cross(E, V)) -> % -> %;
516b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲515b 517b ⊳
map(f: Cross(E,V) -> Cross(E,V))(x: %): % == per map(f) rep x;
516c⟨exports: SparseIndexedPowerProduct 509a⟩+
≡ (506) ⊲516a 518b ⊳
if E has with {-: (%, %) -> %; -: % -> %} then {
⟨exports: SparseIndexedPowerProduct divide 517a⟩
}
Export of SparseIndexedPowerProduct
/: (%, %) -> %
Description
Divides two power products.
Remarks
Note that division is always possible, i. e., the result can contain negative
exponents.
517a⟨exports: SparseIndexedPowerProduct divide 517a⟩≡ (516c)
/: (%, %) -> %;
517b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲516b 519b ⊳
if E has with {-: (%, %) -> %; -: % -> %} then {
⟨implementation: SparseIndexedPowerProduct divide 517c⟩
}
517c⟨implementation: SparseIndexedPowerProduct divide 517c⟩≡ (517b)
(x: %) / (y: %): % == per(X - Y);
Export of SparseIndexedPowerProduct
apply: (%, V) -> E
Usage
macro Z == Integer;
macro T == SparseIndexedPowerProduct(Z, Z);
t: T := power(2, 1) * power(3, 2) * power(5, 1); -- 2*9*5=90
e2: Z := t.2;
e3: Z := t.3;
e4: Z := t.4;
assert(e2=1);
assert(e3=2);
assert(e4=0);
Description
Extracts the exponent corresponding to some variable.
A power product can be seen as a function (with finite support) f : V → E.
apply(f,v) or f.v simply returns f(v) for some variable v ∈ V .
Remarks
If v is not in the power product f, i. e., v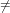 suppf, then f(v) = 0.
suppf, then f(v) = 0.
518a⟨exports: SparseIndexedPowerProduct apply 518a⟩≡ (518b)
apply: (%, V) -> E;
518b⟨exports: SparseIndexedPowerProduct 509a⟩+
≡ (506) ⊲516c 520b ⊳
if E has with {0: %} then {
⟨exports: SparseIndexedPowerProduct apply 518a⟩
}
519a⟨implementation: SparseIndexedPowerProduct apply 519a⟩≡ (519b)
apply(x: %, v: V): E == apply(X, v);
519b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲517b 521b ⊳
if E has with {0: %} then {
⟨implementation: SparseIndexedPowerProduct apply 519a⟩
}
Export of SparseIndexedPowerProduct
divisors: % -> Generator %
Usage
macro Z == Integer;
macro T == SparseIndexedPowerProduct(Z, Z);
t: T := power(2, 1) * power(3, 2) * power(5, 1); -- 2*9*5=90
for d in divisors t repeat {
for ep in d repeat {
(e, p) := ep;
stdout << "(" << p << "^" e ")";
}
stdout << newline;
}
Description
Generates all divisors.
The function divisors returns all divisors of the given element. If p = ∏
i=1nviei
with vi ∈ V , ei ∈ E then a divisor of p is an element q = ∏
i=1nviai such that
0 ≤ ai ≤ ei. The function divisors returns all such q.
520b⟨exports: SparseIndexedPowerProduct 509a⟩+
≡ (506) ⊲518b 521c ⊳
if E has with {0: %; next: % -> %} then {
⟨exports: SparseIndexedPowerProduct divisors 520a⟩
}
521a⟨implementation: SparseIndexedPowerProduct divisors 521a⟩≡ (521b)
divisors(x: %): Generator % == generate {
one? x => yield x;
ev := leadingMonomial X;
(e, v) := ev;
for d in divisors per reductum X repeat {
i: E := 0;
while i <= e repeat {
yield power(v, i) * d;
i := next i;
}
}
}
Uses Generator 617.
521b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲519b 522b ⊳
if E has with {0: %; next: % -> %} then {
⟨implementation: SparseIndexedPowerProduct divisors 521a⟩
}
521c⟨exports: SparseIndexedPowerProduct 509a⟩+
≡ (506) ⊲520b 523a ⊳
if V has with {weight: % -> E} and E has with {0: %; *: (%, %) -> %} then {
⟨exports: SparseIndexedPowerProduct weight 522a⟩
}
Export of SparseIndexedPowerProduct
weight: % -> E
Description
Computed the weight of a power product.
We assume that the weight of a variable xj is wj = weight(xj). Then the weight of a
monomial ∏
j=1nxjaj is given by
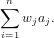 |
(181)
|
522a⟨exports: SparseIndexedPowerProduct weight 522a⟩≡ (521c)
weight: % -> E;
522b⟨implementation: SparseIndexedPowerProduct 509b⟩+
≡ (506) ⊲521b 523b ⊳
if V has with {weight: % -> E} and E has with {0: %; *: (%, %) -> %} then {
⟨implementation: SparseIndexedPowerProduct weight 522c⟩
}
522c⟨implementation: SparseIndexedPowerProduct weight 522c⟩≡ (522b)
weight(x: %): E == {
z: E := 0;
for ev in X repeat {
(e, v) := ev;
z := z + weight(v) * e;
}
z;
}
524⟨implementation: SparseIndexedPowerProduct output 524⟩≡ (523b)
#if Axiom
local term(e: E, v: V): OutputForm == {
if E has with { OutputType; one?: % -> Boolean }
then {
if one? e
then tw := v::OutputForm
else tw := v::OutputForm ** e::OutputForm;
}
else tw := v::OutputForm * e::OutputForm;
}
coerce(x: %): OutputForm == {
import from V, E, String, OutputForm;
one? x => message "1";
y: Rep := rep x;
(e, v) := leadingMonomial y;
y := reductum y;
tw := term(e, v);
while not zero? y repeat {
(e, v) := leadingMonomial y;
tw := tw * term(e, v);
y := reductum y;
}
tw;
}
#endif
(tw: TextWriter) << (x: %): TextWriter == {
import from V, E, String;
one? x => tw << "1";
y: Rep := rep x;
(e, v) := leadingMonomial y;
y := reductum y;
tw := tw << v << "^" << e;
while not zero? y repeat {
(e, v) := leadingMonomial y;
tw := tw << "*" << v << "^" << e;
y := reductum y;
}
tw;
}
Uses OutputType 570 and String 65.
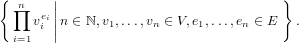
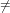 v2 then
v1e1v2e2 = v2e2v1e1. However, depending on whether the + operation in E is
commutative or not it could well be that
v2 then
v1e1v2e2 = v2e2v1e1. However, depending on whether the + operation in E is
commutative or not it could well be that 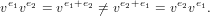
 supp
supp