Definition 10.4 ([BLL98, p. 13]). The generating series or exponential generating series of a species of structures F is the formal power series
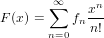 | (125) |
Definition 10.4 ([BLL98, p. 13]). The generating series or exponential generating series of a species of structures F is the formal power series
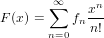 | (125) |
Usage
f: ExponentialGeneratingSeries := monom;
s: DataStream Integer := ...
g := s :: ExponentialGeneratingSeries;
Description
Exponential generating series.
ExponentialGeneratingSeries is the domain that represents exponential generating series, i. e., formal power series f of the form
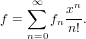 | (126) |
Exports of ExponentialGeneratingSeries
FormalPowerSeriesCategory Fraction Integer;
factorialStream: DataStream Integer Provides a stream of factorials.
count: (%, MachineInteger) -> Integer Counts the number of structures of a given size.
functorialCompose: (%, %) -> % Functorial composition of two series.
Export of ExponentialGeneratingSeries
factorialStream: DataStream Integer
Description
Provides a stream of factorials.
Export of ExponentialGeneratingSeries
count: (%, MachineInteger) -> Integer
Description
Counts the number of structures of a given size.
Export of ExponentialGeneratingSeries
functorialCompose: (%, %) -> %
Description
Functorial composition of two series.
If
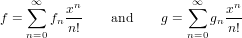 |
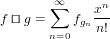 | (127) |
The best guess for the approximate order of the result without accessing any coefficient is 0. So we can simply use coerce.