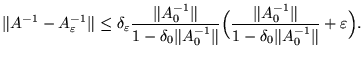Next: Bibliography
Up: Exact Real Computation in
Previous: Vectors, matrices
Let
 be a nonsingular matrix with a known
approximation
be a nonsingular matrix with a known
approximation
 . We
determine first the forward error:
. We
determine first the forward error:
 |
(1) |
We have to find an upper bound for
 , so by using
inequality 1 we get
yielding
whenever
, so by using
inequality 1 we get
yielding
whenever
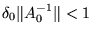 . Because
. Because 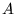 is nonsingular,
is nonsingular,
 converges to
converges to
 as
as  goes
to zero, thus the previous condition can be fulfilled within finitely
many iterative refinements of the approximation
goes
to zero, thus the previous condition can be fulfilled within finitely
many iterative refinements of the approximation 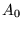 of
of 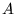 .
.
Assuming that
 is an approximation with
is an approximation with
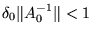 , for the forward error we get
, for the forward error we get
In the backward error computation, given
 , we determine
, we determine
 such that
such that
 implies
implies
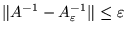 . We apply inequality 1 for
. We apply inequality 1 for 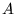 and
and
 :
:
and because
 ,
using the upper bound for
,
using the upper bound for
 , we write:
If we choose
, we write:
If we choose
 such that the above product is
less than
such that the above product is
less than
 , we can compute an
, we can compute an
 -approximate
for
-approximate
for  from
from
 . For instance, we may set
. For instance, we may set



Next: Bibliography
Up: Exact Real Computation in
Previous: Vectors, matrices
![]() be a nonsingular matrix with a known
approximation
be a nonsingular matrix with a known
approximation
![]() . We
determine first the forward error:
. We
determine first the forward error:

![]() is an approximation with
is an approximation with
![]() , for the forward error we get
, for the forward error we get

![]() , we determine
, we determine
![]() such that
such that
![]() implies
implies
![]() . We apply inequality 1 for
. We apply inequality 1 for ![]() and
and
![]() :
: